Lagrange插值练习题

[toc]

XOR Sum

设f(i, k) = 1 \bigoplus 2 \bigoplus 3 ...\bigoplus i^k
给定三个整数t, x, y, 求下面公式对1e9+7取模的值。

\sum_{k=1}^{t} \sum_{i=x}^{y} f(i, k)

拉格朗日插值求解。。
首先分析f函数，发现：

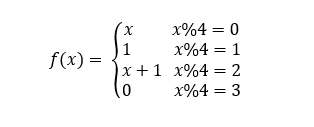
可以据此来推公式
\sum_{k=1}^{t} \sum_{i=x}^{y} f(i, k) = \sum_{k=1}^{t} \sum_{i=1}^{y} f(i, k) - \sum_{k=1}^{t} \sum_{i=1}^{x-1} f(i, k)
\sum_{k=1}^{t} \sum_{i=1}^{x} f(i, k) = \sum_{k=1}^{t} \sum_{i=1}^{x} i^k[i^k\%2==0] + \sum_{k=1}^{t} \sum_{i=1}^{x} [i^k\%4 == 1 or 2]
对于上式

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const ll maxn = 1e5+5, mod = 1e9+7;
ll t, a, b;
ll pre[maxn], suf[maxn], fac[maxn], y[maxn];
ll pow_mod(ll a, ll b){
    a %= mod, b %= mod-1;
    if (!a) return 0;
    ll ans = 1;
    while (b){
        if (b&1)    ans = ans*a%mod;
        b >>= 1;
        a = a*a%mod;
    }
    return ans;
}
ll inv(ll a){
    a = (a%mod+mod)%mod;
    return pow_mod(a, mod-2);
}
ll Lagrange(ll x){
    ll ans = t*(x/4%mod+((x%4)?1:0)) + x/4%mod + (x%4>=2) + t/2*(x/4%mod+(x%4>=3));
    pre[0] = suf[t+2+1] = 1;
    x /= 2;     x %= mod;
    for (int i=1; i<=t+2; i++)  pre[i] = pre[i-1]*(x-i)%mod;
    for (int i=t+2; i>=1; i--)  suf[i] = suf[i+1]*(x-i)%mod;
    for (int i=1; i<=t+2; i++){
        int flag = 1;
        if ((t+2-i)&1)  flag = -1;
        ans = (ans + y[i]*pre[i-1]%mod*suf[i+1]%mod*inv(fac[i-1])%mod*inv(fac[t+2-i])%mod*flag)%mod;
    }
    return ans;
}

int main(){
    ll ans;
    cin >> t >> a >> b;
    fac[0] = 1;
    for (int i=1; i<=t+3; i++)  fac[i] = fac[i-1]*i%mod;
    for (ll i=1; i<=t+2; i++)  y[i] = (y[i-1]+2*i*(pow_mod(2*i, t)-1)%mod*inv(2*i-1)%mod)%mod;
    ans = Lagrange(b) - Lagrange(a-1);
    ans = (ans%mod+mod)%mod;
    cout << ans;
    return 0;
}